On the Day of cosmonautics! We passed to the printer “a Small book about black holes”. In these days of astrophysics showed the world how black holes look like. Coincidence? I don’t think 😉 So wait, soon there will be an amazing book, which was written by Steven Gubser, and Frans Pretorius, translated wonderful Pulkovo astronomer aka Astrodad Kirill Maslennikov, made scientific editing of the legendary Vladimir Surdin and supported her publishing the Fund’s Trajectory.
Excerpt “the Thermodynamics of black holes” under the cut.
So far we have considered black holes as astrophysical objects, which were formed by supernova explosions or lie in the centers of galaxies. We see them indirectly, by measuring the acceleration close to them stars. Famous the detection of gravitational waves LIGO receiver 14 Sep 2015 has become an example of more direct observations of the collision of black holes. The mathematical tools we use to achieve a better understanding of the nature of black holes, these are: differential geometry, Einstein equations and powerful analytical and numerical methods applied for solving the Einstein equations to describe the geometry of space-time which give rise to black holes. And once we are able to give a full quantitative description generated by black hole space-time, from astrophysical point of view, the topic of black holes can be considered closed. In a broader theoretical perspective there are still many opportunities for research. The aim of this Chapter is to describe some of the theoretical achievements of modern physics of black holes, in which the ideas of thermodynamics and quantum theory combined with the General theory of relativity, giving rise to unexpected new concept. The basic idea is that black holes are not just geometrical objects. They have temperature, they have a huge entropy and can demonstrate quantum entanglement. Our reasoning about thermodynamic and quantum aspects of the physics of black holes will be more fragmented and superficial than those presented in the previous chapters the analysis of the purely geometrical features of space‑time in black holes. But these, and especially the quantum aspects are essential and a vital part of the ongoing theoretical studies of black holes, and we really try to convey if not the intricate details, then at least the spirit of these works.
In classical General relativity — if we talk about differential geometry of solutions of Einstein equations black holes are truly black in the sense that from them nothing can get out. Stephen Hawking showed that this situation completely changes when we take into account quantum effects: black holes, it turns out, emit radiation of a certain temperature, known as the Hawking temperature. For black holes of astrophysical size (i.e., from black holes stellar-mass to supermassive), the Hawking temperature is negligible compared to the temperature of the cosmic microwave background radiation that fills the entire Universe, which, incidentally, itself can be considered as a variant of Hawking radiation. The calculations performed to determine the Hawking temperature of black holes, are part of a broader programme of research in a field called thermodynamics of black holes. Another big part of this program is the study of the entropy of black holes, which characterizes the amount of information is lost inside a black hole. Ordinary objects (such as a Cup of water, a bar of pure magnesium or a star) also have entropy, and one of the Central claims of the thermodynamics of black holes is that a black hole of this size has greater entropy than any other form of matter that can be accommodate in the region of the same size, but without the formation of a black hole.
But before we deep dive into the analysis of problems related to Hawking radiation and entropy of black holes, let’s take a quick excursus in the field of quantum mechanics, thermodynamics and entanglement. Quantum mechanics was developed mainly in the 1920-ies, and its main goal was the description of very small particles of matter such as atoms. The development of quantum mechanics led to the erosion of such basic concepts of physics, as the exact position of individual particles: for example, that the position of an electron during its motion around an atomic nucleus cannot be precisely determined. Instead, the electrons were assigned to the so-called orbits in which their actual position can be determined only in a probabilistic sense. For our purposes, however, it is important not to jump to this probability — side of things too quickly. Take the simplest example: hydrogen atom. It may be in a defined quantum state. The most simple as the hydrogen atom, called the primary, is the lowest energy state and this energy is precisely known. In a more General sense, quantum mechanics allows us (in principle) know the state of any quantum system exactly.
Probability go on stage, when we ask certain questions about quantum mechanical system. For example, if definitely known that the hydrogen atom in the ground state, we can ask: “Where is the electron?” and according to the laws of quantum
mechanics will receive to this question, just some assessment of probability, something like: “probably, the electron is at a distance of up to half Angstrom from the nucleus of the hydrogen atom” (one Angstrom is equal to 
meters). But we have the ability through a physical process to find the position of the electron better than one Angstrom. This is quite common in the physics of the process is to run in the electron a photon with very short wavelength (or, as physicists say, to dissipate the photon on the electron) — then we will be able to reconstruct the location of the electron at the moment of scattering with an accuracy approximately equal to the wavelength of the photon. But this process will change the state of an electron, so then it won’t already be in the ground state of the hydrogen atom and will not have a precisely defined energy. But for a while it will be almost exactly determined (up to a wavelength used for the photon). Preliminary assessment of the status of the electron can be carried out only in a probabilistic sense, with an accuracy of about one Angstrom, but once we measured it, we know exactly what it was. In short, if we in some way measure a quantum mechanical system, at least in the conventional sense, we “forced” to give her a condition with a specific value of that measure.
Quantum mechanics applies not only to small but (we believe) to all systems, but for larger systems, quantum mechanical rules quickly become very complex. The key concept is quantum entanglement, a simple example which can serve as the concept of spin (rotation). Individual electrons have spin, so in practice a single electron can have spin pointing up or down relative to a selected spatial axis. The electron spin is an observable quantity because the electron generates a weak magnetic field similar to magnetic field of the bar. Then the spin is directed upwards, means that the North pole of the electron is pointing down, and the spin pointing down, means that the North pole is up. Two electrons can be placed in paired quantum state in which one of them has spin pointing up and the other down, but to say, some of the electrons which spin when this is not possible. In fact, in the ground state of the helium atom two electrons are in that state called a spin singlet, since the total spin of both electrons is zero. If we divide these two electrons, without changing their spins, will be able to continue to claim that they together spin-singlet, but still can’t say what will be the spin from any of them individually. Now, if we measure one of them spins and the install that it is directed upward, then we are absolutely sure that the second pointing down. In this situation we say that the spins are entangled — neither one by itself has no defined value, while together they are in a particular quantum state.
Einstein was very troubled by the phenomenon of entanglement: it seemed to threaten the basic principles of the theory of relativity. Consider the case of two electrons in a spin-singlet state when they are separated far from each other in space. For definiteness, let one of them get Alice and the other Bob. Suppose that Alice has measured the spin of his electron and found that it is pointing up, and Bob is nothing to measure did not. While Alice did not fulfill its dimension, it was impossible to say what the spin of its electron. But as soon as she their dimension made up, she certainly learned that the electron spin of Bob is pointing down (in the direction opposite the direction of spin of her electron). Does this mean that its measurement is instantly transferred electron Bob’s state when its spin is pointing down? How could this occur if the electrons are spatially separated? Einstein and his collaborators, Nathan Rosen and Boris Podolsky felt that the story with the measurement of entangled systems is so serious that it threatens the very existence of quantum mechanics. They formulated the Einstein—Podolsky—Rosen (EPR) uses a thought experiment similar to the one we have just described, to conclude that quantum mechanics cannot be a complete description of reality. Now on the basis of the subsequent theoretical research and numerous measurements have established the General opinion that the EPR paradox contains an error, and quantum theory is correct. Quantum-mechanical entanglement of the real: the measurement of entangled systems are correlated, even if these systems far apart in space-time.
Back to the situation where we put two electrons in a spin-singlet state and gave them to Alice and Bob. What can we say about electrons before the measurements? Both together they are in a specific quantum state (spin-singlet). Alienage spin of the electron with equal probability of pointing up or down. More precisely, the quantum state of the electron with equal probability can be one (spin-up) or the other (spin down). Now for us the concept of probability acquires a deeper meaning than before. First, we have considered certain quantum state (the ground state of the hydrogen atom) and saw that there are some “uncomfortable” questions, such as “Where is the electron?”, — the questions, the answers to which exist only in a probabilistic sense. If we were asking “good” questions, such as: “What is the energy of this electron?”, we would get them some answers. Now there are no good questions we could ask about Alisina electron, the answers to which would not depend on the electron Bob. (We’re not talking about stupid questions like, “do Alienage electron actually spin?” — questions to which there is only one answer.) Thus, to determine the parameters of one of the halves of a confusing system we have to use probabilistic language. Certainty arises only when we consider the relationship between the questions that you can ask about their electrons Alice and Bob.
We purposely started with one of the simplest quantum mechanical systems, which are known to us: system of spins of individual electrons. It is hoped that on the basis of such simple systems will be built quantum computers. The system of spins of individual electrons or other equivalent quantum systems called qubits (short for “quantum bits”), which emphasizes their role in quantum computers, similar to the role played by ordinary bits in digital computers.
Imagine now that we have replaced each electron is much more complex quantum system with many, not just two quantum States. For instance, given Alice and Bob are bars of pure magnesium. Before Alice and Bob will go about their business in different directions, their bars can interact, and we agree, that when they acquire a certain common quantum state. As soon as Alice and Bob disagree, their magnesium bars cease to interact. As in the case of electrons, each bar is in an indeterminate quantum state, although together, we believe they form as a definite. (In this discussion we assume that Alice and Bob are able to move their magnesium bars, not disturbing their internal state, similarly as before we have assumed that Alice and Bob could share their entangled electrons, without changing their spins.) But the difference between this thought experiment and the experiment with electrons is that the uncertainty of the quantum state of each block is huge. The bar may well purchase more quantum States than the number of atoms in the Universe. Here on the stage and out the thermodynamics. A very ill-defined system can, however, have some well-defined macroscopic characteristics. Such a characteristic is, for example, temperature. Temperature is a measure of the probability with which any part of the system has a definite average energy, and higher temperatures correspond to greater probability to have more energy. Another thermodynamic parameter, the entropy essentially equal to the logarithm of the number of States that the system can accept. Another thermodynamic characteristics that would be essential for the bar of magnesium is its total magnetization, that is, in essence, a parameter showing how much more the bar can be electrons with spin directed upwards, than with the spin pointing down.
We are attracted to our story of thermodynamics as a way to describe the system quantum States which are not precisely known because of their entanglement with other systems. Thermodynamics is a powerful tool for the analysis of such systems, but its creators did not foresee such applications. Sadi Carnot, James Joule, Rudolf Clausius was the figures of the industrial revolution of the nineteenth century, and were interested in their most practical of all questions: how do the engines? Pressure, volume, temperature and warmth, flesh and blood engines. Carnot found that the energy in the form of heat can never be converted completely into useful work, like lifting. Part of the energy will always be wasted. Clausius contributed to the creation of the idea of entropy as a universal tool for determining the energy losses in the course of any process associated with warmth. His main achievement was the realization that entropy never decreases — almost all processes it is growing. Processes in which entropy increases are called irreversible because they can’t go backwards without reducing entropy. The next step towards the development of statistical mechanics was made by Clausius, Maxwell and Ludwig Boltzmann (among many others) — they showed that entropy is a measure of disorder. Usually the more you act on something, the more there are making the mess. And even if you have developed a process, which aims to restore order in the course of his inevitably produces more entropy than is destroyed — for example, if release of heat. A crane, which puts steel beams in perfect order, creates order in the sense of the location of the beams, but in the course of his work stand out so much heat that the total entropy is still increasing.
But the difference of opinion on the thermodynamics of physicists of the XIX century from the look associated with quantum entanglement, not as great as it seems. Each time the system interacts with the external agent, its quantum state becomes entangled with the quantum state of the agent. Usually this confusion leads to an increase of uncertainty of the quantum state of the system, in other words, to increase the number of quantum States in which the system can be. As a result of interaction with other systems the entropy, defined in terms of the number of available quantum States, usually growing.
In General, quantum mechanics provides a new way to characterize a physical system in which some parameters (such as position in space) is undefined, but others (for example, energy) is often known precisely. In the case of quantum entanglement of two fundamentally separate parts of the system are known, the total quantum state, and each part separately — as uncertain. A standard example of entanglement is a pair of spins in a singlet state in which it is impossible to tell which spin is pointing up and some down. The uncertainty of a quantum state in a large system requires a thermodynamic approach, in which macroscopic parameters such as temperature and entropy, are known with great precision, despite the fact that the system there are many possible microscopic quantum States.
After our brief excursion into the area of quantum mechanics, entanglement and thermodynamics, let us now try to understand how all this leads to the understanding of the fact that black holes have a temperature. The first step to this direction was made by bill Unruh — he showed that an accelerating observer in flat space will have a temperature equal to its acceleration divided by 2π. The key to calculating Unruh that the observer moving with constant acceleration in a particular direction, can only see half of the flat space‑time. The second half, in fact, is over the horizon, like the horizon of a black hole. At first it seems impossible: how can a flat space-time to behave like the horizon of a black hole? To understand how this goes, let us invoke the aid of our faithful observers Alice, Bob, and bill. At our request, they line up, and Alice is among Bob and bill and between the observers in each pair the distance is exactly 6 miles. Agreed that at time zero, Alice will jump into a rocket and fly to bill (and hence Bob) with a constant acceleration. Rocket is very good at it, capable of developing an acceleration of 1.5 trillion times greater than the gravitational acceleration with which objects move near the Earth’s surface. Of course, to withstand such acceleration Alice isn’t easy, but, as we shall see, these numbers are chosen with a certain aim; in the end, we’re just discussing the potential, that’s all. At exactly the moment when Alice leaps to his rocket, Bob and bill waving her hand. (We may use the expression “at exactly the moment when…” because while Alice has not yet begun flying, she is in the same frame of reference that Bob, bill, so all they can synchronize their clock.) Bill waving at her Alice, of course, sees the truth, while in the rocket, she will see him before this would have happened if she had stayed where was, because her rocket with her flying to him. From Bob she, on the contrary, is deleted, so we can reasonably assume that she will see him waving at her, a little later than would see it stay in the same place. But the truth is even more surprising: Bob she did not see! In other words, photons, which fly from the waving Bob to Alice will never catch up, even though it can never reach the speed of light. If Bob has started to swing, being a little closer to Alice, then the photons which flew away from him at the time of her departure, she would be caught, and if he was a little further, especially not overtaken. It is in this sense we say that Alice is only visible half of the space-time. At the time when Alice moves, Bob is slightly further to the horizon, watching Alice.
In our discussion of quantum entanglement we have become accustomed to the idea that even if a quantum mechanical system as a whole has some quantum state, some of its parts can not have. In fact, when we are discussing complex quantum system, some part of it can best be described in the framework of thermodynamics: it can be assigned a well-defined temperature, in spite of highly uncertain quantum state of the entire system. Our last story involving Alice, Bob, and bill looked a little like this situation, but the quantum system, which we are talking about here, is the empty space-time, and Alice sees only a half. Stipulate that the space-time in General is in its ground state, which means the absence of particles (of course, not counting Alice, Bob, bill and missiles). But the part of space-time, which sees Alice, will be in the ground state and in a state of confused with that part of it which she sees. Alice perceived space-time is a complex indeterminate quantum state characterized by a finite temperature. Unruh calculations show that this temperature is approximately 60 nanokelvins. In short, as the acceleration Alice as if dipped in a warm bath of radiation with temperature equal (in appropriate units) acceleration divided by 
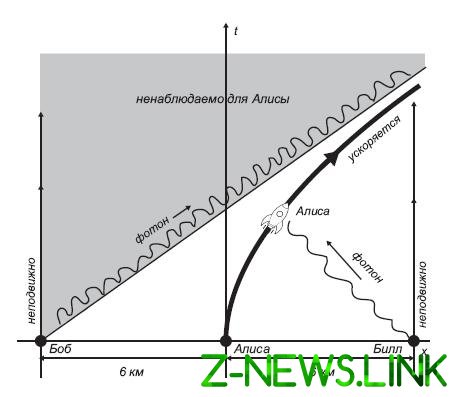
Fig. 7.1. Alice is accelerated from rest, while Bob and bill remain stationary. The acceleration of Alice such that she never saw a photon, which sends it in the direction of the Bob at time t = 0. However, it receives photons which at time t = 0 she sent bill. The result is that Alice is able to observe only one half of space‑time.
The strangeness of the Unruh calculations is that although they are from start to finish related to empty space, they contradict the well-known words of king Lear “nothing will come of nothing”. How can empty space be so difficult? Where it can take particles? The fact is that according to quantum theory, empty space is not empty. In it here and there constantly appear and disappear short-lived excitation, called virtual particles, whose energy can be both positive and negative. The observer from the distant future — let’s call her Carol, who is able to see virtually all empty space can confirm that there are no long existing particles. The presence of particles with positive energy in that part of space-time that Alice can observe, thanks to quantum entanglement is associated with excitations of equal and opposite sign of the energy unobservable at for Alice’s part of space‑time. The truth about empty space-time in General open for Carol, and this truth is that there are no particles. However, the experience of Alice and tells her that the particles are there!
But then it turns out that the computed Unruh temperature seems to be just a fiction — it is not so much a property of flat space itself, as a property of the observer facing in a flat space of constant acceleration. However, the very gravity is a “fictitious” force in the sense that “acceleration” which they invoked, there is nothing like movement on a geodesic in curved metric. As we have explained in Chapter 2, the Einstein equivalence principle is that acceleration and gravity are, in essence, equivalent. From this point of view there is nothing particularly shocking in the fact that the horizon of a black hole has a temperature equal to the calculated Unruh temperature for accelerating observers. But, can we ask what acceleration value should we use to determine temperature? At a sufficiently large distance from the black hole, we can make its gravitational attraction is arbitrarily weak. Does it follow that to determine the measured effective temperature of a black hole we need to use a proper small value of acceleration? This question is quite tricky, in fact, we believe, the object temperature can be arbitrarily reduced. It is assumed that it has some fixed finite value, which can measure even very remote observer.
© 2019, paradox. All rights reserved.
